LeetCode (C/C++) 1314. Matrix Block Sum

https://leetcode.com/problems/matrix-block-sum/

---

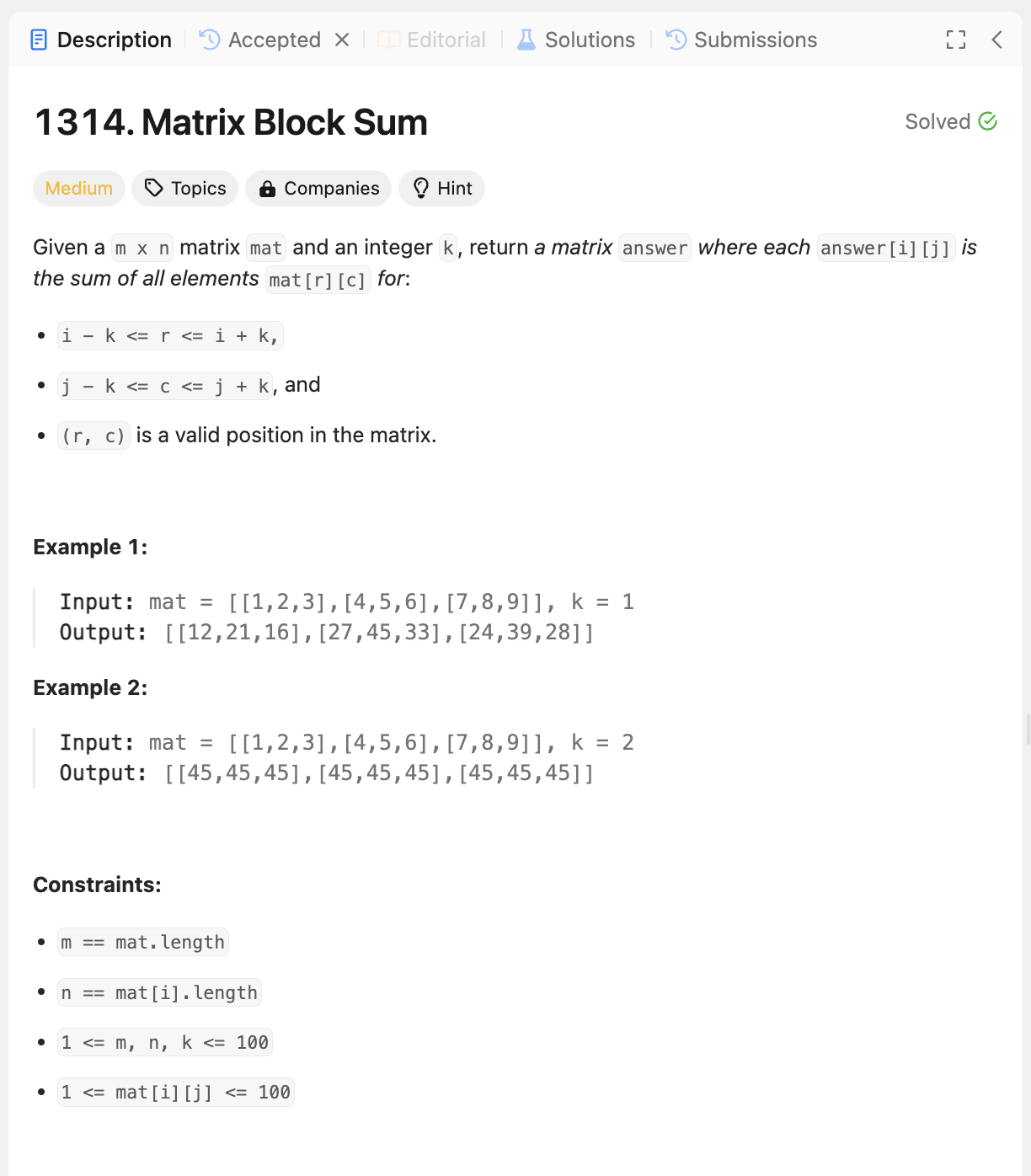
풀이

문제의 요구사항을 그대로 구현했더니 시간이 오래 걸려서 누적합 방식으로 다시 풀었다.

---

코드 1 - 요구사항 그대로

class Solution {
public:
    vector<vector<int>> matrixBlockSum(vector<vector<int>>& mat, int k) {
        int m = mat.size(), n = mat[0].size();
        vector<vector<int>> ans;
        for (int i = 0; i < m; i++) {
            vector<int> col;
            for (int j = 0; j < n; j++) {
                col.push_back(getAnswer(max(0, i - k), min(i + k, m - 1), max(j - k, 0), min(j + k, n - 1), mat));
            }
            ans.push_back(col);
        }
        return ans;
    }

    int getAnswer(int r1, int r2, int c1, int c2, vector<vector<int>>& mat) {
        int sum = 0;
        for (int r = r1; r <= r2; r++) {
            for (int c = c1; c <= c2; c++) {
                sum += mat[r][c];
            }
        }
        return sum;
    }
};

 

코드 2 - 누적합

class Solution {
public:
    vector<vector<int>> matrixBlockSum(vector<vector<int>>& mat, int k) {
        int m = mat.size(), n = mat[0].size();
        int sum[101][101] = {0, };

        sum[0][0] = mat[0][0];
        for (int i = 1; i < m; i++) sum[i][0] = mat[i][0] + sum[i - 1][0];
        for (int j = 1; j < n; j++) sum[0][j] = mat[0][j] + sum[0][j - 1];

        for (int i = 1; i < m; i++) {
            for (int j = 1; j < n; j++) {
                sum[i][j] = mat[i][j] + sum[i - 1][j] + sum[i][j - 1] - sum[i - 1][j - 1];
            }
        }
        vector<vector<int>> ans;
        for (int i = 0; i < m; i++) {
            vector<int> col;
            for (int j = 0; j < n; j++) {
                int val = sum[min(i + k, m - 1)][min(j + k, n - 1)];
                int flag = 0;
                if (i - k - 1 >= 0){
                    val -= sum[i - k - 1][min(j + k, n - 1)];
                    flag++;
                }
                if (j - k - 1 >= 0){
                    val -= sum[min(i + k, m - 1)][j - k - 1];
                    flag++;
                }
                if (flag == 2)
                    val += sum[max(i - k - 1, 0)][max(j - k - 1, 0)];
                col.push_back(val);
            }
            ans.push_back(col);
        }
        return ans;
    }
};